《概率论与数理统计》

“课程思政”典型教学案例（一）

课程名称：概率论与数理统计                    学时：48                   学分：3

课程类别：公共类                              授课对象：工科、管理类各专业学生

课程负责人：王芬                              课程组成员：商培培、陈雪丽、李慧慧、方慧文、陈少军

    1.案例主题：中心极限定理背后的哲学观

2.结合章节：5.2中心极限定理

3.案例意义：

中心极限定理描述在相当一般的条件下，大量独立随机变量的和近似服从正态分布。首先定理表明，无论随机变量是否服从正态分布，只要满足一定的条件，随着随机变量个数的增加，随机变量和的分布总是逐渐收敛于正态分布。从杂乱无章到工整的正态分布，正是由量变引发了质变。其次，随机变量的分布具有偶然性,而一定条件下,大量独立随机变量的和近似服从正态分布，具有必然性。随机变量本身的分布与正态分布可能截然不同，这体现了偶然性与必然性的对立，而这些大量的独立随机变量之和的极限分布总是正态分布，这体现了偶然性与必然性的统一，这也就是说中心极限定理揭示了偶然性与必然性的对立统一。

4.案例描述：

（1）教学目标

知识目标：掌握常用的中心极限定理；

能力目标：能利用中心极限定理近似计算概率；

素质目标：培养学生的探索精神、观察总结的习惯，挖掘中心极限定理背后的哲学思想。

（2）教学内容

教学知识点：常用的中心极限定理及其在概率计算中的应用；

教学重点：独立同分布的中心极限定理和棣莫弗－拉普拉斯定理；

教学难点：利用中心极限定理近似计算概率。

（3）教学方法

讲授法与课堂讨论练习结合

（4）教学过程设计

①课堂导入：由问题“若某个随机变量是由大量相互独立且均匀小的随机变量相加而成的,其概率分布情况如何？”引出中心极限定理的背景意义，即在一定条件下，大量独立随机变量和近似服从正态分布。

    ②独立同分布的中心极限定理及其应用

    首先给独立同分布的中心极限定理：

    定理1 设随机变量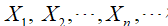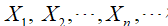相互独立,服从同一分布,且具有数学期望和方差：

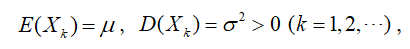
则随机变量之和的标准化变量

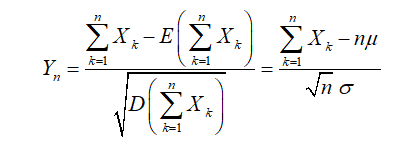
的分布函数对于任意实数x满足

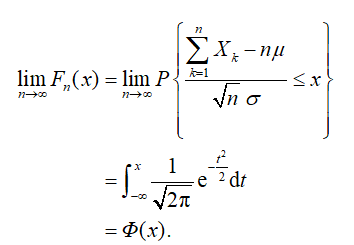
    再进一步对定理进行解释说明，辅助学生理解。

    其次，引导学生利用正态分布的性质，得到定理1结论的几种不同形式：

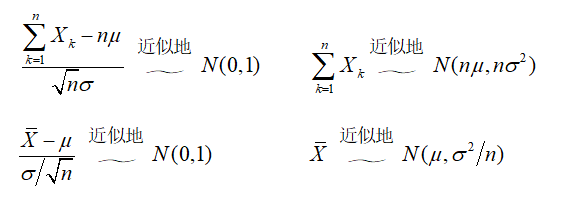
最后，给出例题，让学生体会定理1在具体概率问题中的应用，引导学生总结解题方法，再给出例题让学生自行求解。

思政元素挖掘：通过例题和练习，让学生体会到由观察分析到归纳方法再到应用的思维方式，逐步养成观察总结的习惯。

    ③李雅普诺夫定理

此定理不重点讲解，只解释其背景意义。

    ④棣莫弗－拉普拉斯定理

    首先，引导学生思考定理1中随机变量独立同分布于(0-1)分布时的情形，让学生自行推出棣莫弗－拉普拉斯定理如下：

定理3 设随机变量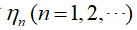服从参数为n,p(0<p<1)的二项分布,则对于任意x,有

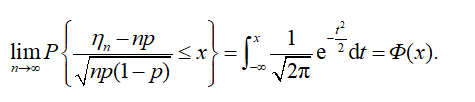
以此激发学生学习热情，培养学生探索精神。

思政元素挖掘：借助两定理之间的关系提醒学生在日常生活与学习中，要积极探索事物之间的联系，并利用这些联系进行延伸思考。

其次，给出二项分布与正态分布的图像对比如下：

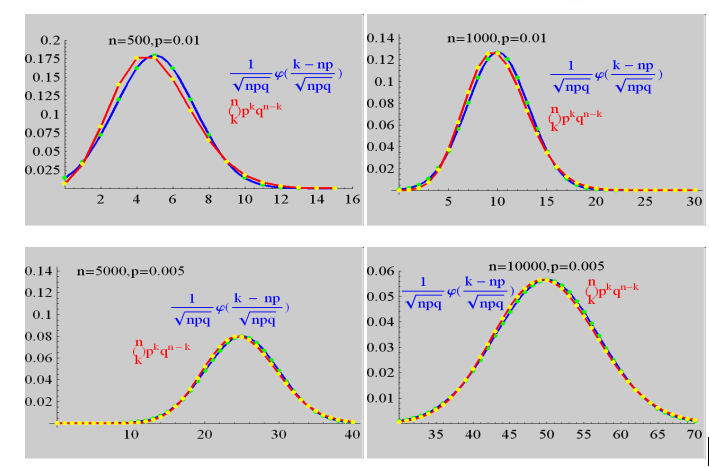
利用图像，让学生能更为直观地观察到二项分布的正态近似，引导学生思考中心极限定理所揭示的哲学观。

思政元素挖掘：只要满足一定条件，无论随机变量服从什么分布，随着个数的增加，随机变量和的分布总是逐渐收敛于正态分布。由此引导学生思考量变与质变的关系，当量变达到一定程度就一定会引发质变。

最后，给出例题，让学生仿照前面总结的方法举一反三解题，让学生体会定理3在具体概率问题中的应用。

    ⑤教学小结

    总结本节所学的三个中心极限定理，回顾定理在具体概率问题中的应用方法、定理所蕴含的哲学思想。

5.学生评价：

    学生表示学习了中心极限定理以后，在老师的引导下，思考了其背后所隐含的哲学观——量变引起质变，明白了目标的实现是依赖于脚踏实地的，无论做什么都要注重量的积累。以前总是空有目标却忽略了眼前小事，比如只想着考研却不在意目前基础数学课程的学习，认为考研数学题目难度大、考察面广，而大学所学知识基础、题目简单，即使学好了到考研时也没有帮助。现在体会到只有一步一个脚印埋头苦干，夯实基础，才能为后续专业课程的学习打下基础，也能在日后复习考研时不用将精力浪费在基础知识学习上。

6.案例反思：

    本节课提前借助线上教学软件设置预习任务，让学生在课前大致了解本节课的主要教学内容。在课堂上，先是以一问一答的形式激发学生学习热情，讲解中心极限定理的背景意义导入新课。再对知识点进行详细讲解，在讲解基础定理时，不断强调定理的背景意义，从而引导学生思考其背后蕴含的哲学思想并将这些哲学观应用在学习、生活中。精选例题，使得学生掌握基础定理的同时，让所学内容在具体概率问题中得到了应用。课后布置习题，使得课上所学定理、做题方法得到了巩固。本节课讲练结合，充分调动学生的积极性，确保了学生在课堂中的主体地位，完成了本节课的知识目标、能力目标和素质目标。但同时，本节课所学知识较多、内容深奥，思政元素又围绕哲学观展开，使得课程思政有些许突兀。要想做到思政元素顺理成章渗入，要多围绕哲学观点进行论证，借助耳熟能详的名人名言、学生所关心的事物进行举例等方法对其进行解释说明，才能使学生更好地理解感悟。

7.效果与反馈：

    通过自行预习中心极限定理的背景意义、教师在课堂上的讲解，学生掌握了本节课所学习的三个常用的中心极限定理；通过课上例题讲解，学生掌握了独立同分布的中心极限定理和棣莫弗－拉普拉斯定理在解决具体概率问题时的应用场景和应用方法、步骤，而后在课后习题巩固过程中让总结的方法得到了灵活应用，使得学生认识到观察总结的重要性；通过由独立同分布的中心极限定理推出棣莫弗－拉普拉斯定理这一过程，激发了学生的学习热情，培养了学生的探索精神；在教师的引导下，学生体会到中心极限定理背后所蕴含的哲学思想——量变引起质变，借此教育学生，远大理想的实现依赖于脚踏实地，要想成大事必须要从小事做起、从现在做起，注重量的积累，才能收获质的飞跃。